Math Anxiety: Making Room to Breathe

“Don’t do that to me, Professor,” the student said, and everybody laughed, for by this late in the semester, the atmosphere was relaxed. The instructor in question had just reached the point in a worked problem when they could move from reasoning about specific numbers to stating a general principle: x≤y≤z, meaning that y—the value we sought—was always going to be greater than or equal to one value (x) and less than or equal to the other (z). The student who had spoken had earned everyone’s affection over the weeks, open about their difficulties with math, ready to risk being wrong, and to ask obvious questions that others may have been reluctant to owning. They had hung in there, despite presenting a classic case of math anxiety, a syndrome long recognized in the scholarship of teaching and learning.

Among math anxiety’s many symptoms, breathing disruption ranks high: hyperventilation (rapid breathing) and hypoventilation (barely or not breathing). When the energy-conserving parasympathetic nervous system is overtaken by the energy-expending sympathetic nervous system, the long exhalations that decelerate the heart rate are replaced by short, panting puffs from the upper lungs. The timed test provides the perfect environment for math anxiety to flourish. Stress diverts cognitive resources needed for procedural execution, so working memory consequently shrinks.

Self-rated metrics for math anxiety have been in place for decades (Richardson and Suinn). Relatively trivial interventions can yield nontrivial results: deep breathing exercises and positive affirmations have a beneficial impact, as does writing about one’s nerves immediately prior to an exam (Brunyé et al.). More systemic changes require a reorientation in teaching whereby conceptual mistakes are positively rewarded as opportunities for learning; students compose questions instead of answers; students solve problems together rather than perform solo (Boaler).

Return now to that opening scenario to watch it become stereotype incarnate: the student was mature, Black, and female; the teacher, younger, white, and male; her comment was triggered by his shift from a specific set of numbers into symbolic notation. There is robust evidence to demonstrate that certain demographics are consistently underrepresented in the U.S. math community: women and “African-Americans, Hispanics, American Indians, Alaska Natives, and Pacific Islanders,” according to the Mathematical Association of America (MAA) (“Resources for Minority”). Routinely feeling that they do not belong, such groups are particularly vulnerable to math anxiety.

Several remedies for such disparity suggest themselves: appointing more women and people of color in the profession; one-on-one tutorial assistance; research projects about the students’ personal environment; privileging pre-test, low-stakes work over timed tests; assigning group rather than individual work. When all is said and done, however, such strategies “have little to do with mathematics content” (Martin 304). Mathematicians still need to be able to conceptualize, describe, and manipulate abstract objects, and there seems to be a suspicion that, at heart, abstraction is gendered masculine and colored white.

It is possible that the rhetorical immediacy and context-dependence of Black English has misguidedly reinforced such a perception. For poet June Jordan, Black English “devolves from a culture that abhors all abstraction” (Jordan 367). Psychiatrist Alvin Poussaint asks, “Is there a way to say metamorphosis in Ebonics?” (O’Malley). Yet, despite Black English’s avoidance of nominalization and similar verbosities that afflict academic prose, abstract logical reasoning flourishes in vernacular idiom, as linguist William Labov demonstrated half a century ago. Our aim is not to explain the asymptote in Black English but rather to consider a feature characteristic of those very minority cultures historically underrepresented in math—storytelling—and to ask how it may be foregrounded in mathematics, where it is decisively sidelined. Storytelling has been claimed by every culture and ethnic group at some point as the repository of wisdom, practical skills, religious beliefs, and shared identity and values; but when it gets corralled into the category of “fiction,” and when it gets opposed to “fact,” a narrowed concept of truth dispatches storytelling to kindergarten and recreational math. Word problems may supply scenarios but offer none of a plot’s satisfactions. What we do here is tell and retell one story to put the world back into mathematics.

What Stories Do

Whenever we need to explain something we create stories. David Hume famously noted how, around the phenomenon of colliding billiard balls, we spin the tale of causation, because we cannot see one ball actually causing another to move, only the correlation between collision and motion. The more significantly charged the phenomenon, the more intensely people seek to explain it, identify its causes, and weave stories around it (Paulos 57). The intensity symptomizes meaning-making: just as stories have their build-up and denouement, so problems build tension that is released in the critical turn of a solution. Such narratives have affective cores around which energies gather.

Language itself affirms the connection between stories and numbers: narrating and counting use the same vocabulary. The verb “to tell” is as old as English itself and one we usually associate with narrative, as in to tell a story. Another meaning of “tell,” however, and just as old, is to count. Now largely obsolete, the usage remains fossilized in words like “bank-teller” or “telling votes.” Similar lexical overlap occurs when we re-count votes and recount tales. A classic opener for mathematical proofs is “Suppose…”, inviting the reader to enter the narrative much in the same way that “Once upon a time…” does for fairy tales. These linguistic convergences alert us to deep connections between stories and proofs. Some mathematicians have recognized the affinity. “A proof is simply a story,” notes Paul Lockhart (12). Bernard Teissier emphasizes the copula. Proofs are narration: we understand them if and only if we understand them as narratives (233).

There are epic tales, such as Homer’s Odyssey or Andrew Wiles’s proof of Fermat’s Last Theorem, but we focus here on fleeting accounts that fitfully inhabit a larger narrative structure: episodes, anecdotes, step-by-step reasoned explanations within a homework problem. Like lungs expanding against and subsiding into the elastic frame of the ribcage, these momentary stories stretch and contract within narrative systems that hold them in place. In four different ways, we track here the push and pull between story and frame.

First, the anecdote. The word literally means “unpublished,” suggesting that the event it describes happened spontaneously offstage as private, certainly not the stuff out of which grand narratives are made. Yet it also means that the event, unlike a joke, took place. Anecdotes hold a unique position in being simultaneously factual, inconsequential, and worth relating. As Joel Fineman demonstrated with Thucydides’s anecdote-packed History of the Peloponnesian War, such sketches introduce just enough contingency to make the historical grand narrative, which makes the anecdotes meaningful in the first place, appear to unfold incidentally. Anecdotes acquire theoretical significance and causal interconnection by virtue of their discursive matrix. As the overarching narrative makes the anecdote meaningful, the anecdote validates the overarching narrative. Anecdotes share kinship with case studies, which yoke the theoretical with the practical, appealing to the one by analogy with the other (Jonsen and Toulmin).

Second, counterstories. As the term implies, counterstories push back against larger, toxic narratives at work in culture. Legal scholars Richard Delgado and Jean Stefancic speak of the power of counterstories to disrupt the hierarchy between examiner and witness within the courtroom, where “children and certain other witnesses are permitted to testify in the form of an uninterrupted narrative, rather than through question-and-answer examination” (53). When a witness conforms to standard examination procedure, they “just answer the question,” providing mere backchannel to a narrative controlled ultimately by the legal system itself. The relevant point here is less what the witness says than the opportunity counterstories afford them to fill their lungs and take the floor. One needs expanse to tell stories that string their steps across time, that conform to what Aristotle, in the Poetics, observes about tragic plots, namely, that they must be long enough to display the causal relationships between their origination (beginning), complication (middle), and conclusion (end). Such unfolding of events, regardless of the order in which they are recounted, is impossible without time and space.

Third, storying. When a witness (or student) is required to “just answer the question,” their powers of spontaneous invention wither. Native Louisianan Kevin Young grew up “storying,” which is what one does when riffing on a musical theme (e.g., Louis Armstrong’s extempore jazz solos) or when perpetrating an untruth in the service of a higher truth (e.g., Richard Wright’s forged library card to borrow books in the segregated South). Storying is a short melody that makes room for itself within a larger narrative that may be as innocent as a tune or as ominous as systemic discrimination. It involves “making a way out of no way, and making it up as you go along” (Young 17). By re-conditioning whatever lies at hand, storying turns things aside from their discrete, designated uses to build new networks of connection. It re-creates. Storytellers are improvisors. They re-purpose what they do know to solve what they don’t.

Fourth, math stories. Some math stories occur as a series of reasoned steps within the frame of an assigned problem or proof. Like Aristotle’s plot, these steps are arranged into a tightly patterned sequence, the interrelationship between them fully on display. But there is a difference. They might not occur in clock time. As G. E. R. Lloyd observes, the sequentiality of a theorem’s steps need not imply its temporality. Its explanatory stages occur by actualization (energeia) of latent potential and by making explicit what is implicit rather than by the markers of time’s passage—change of location, position, direction, or state—that inflect verbal narratives. This actualization comes closest to a different feature of tragedy noted by Aristotle: anagnoresis [recognition], in which we encounter, as if for the first time, knowledge we already possessed but had failed fully to realize. Like the pause between breaths, anagnoresis occurs outside time’s rhythm, in a momentary epiphany that leaves everything in its wake different.

We cannot tell stories without having first heard them. Stories are performative inasmuch as close listening itself constitutes a kind of retelling. In the same way, mathematics is performative: to understand it means being able to do it, for, as George Polya once aptly observed, mathematics is not a spectator sport (xx). Here, then, is our math story, told and retold.

A Math Story

First, here it is told denuded of all fictional integumentum and posed as an elementary classroom problem.

The Problem: Let X=15 and Y=9. Let 8 be subtracted from X+Y in such a way that X=8 and Y=8. Finally, let 8 be redistributed between X and Y in three different proportions. Provide mathematical reasoning for each of the following three distributions:

a). X=15 and Y=9
b). X=12 and Y=12
c). X=13 and Y=11

The Solution:

Question a) simply adds back each subtrahend, thereby returning the distributions to their original values:

Question b) simply halves the combined subtrahends and adds one half each to X and Y.

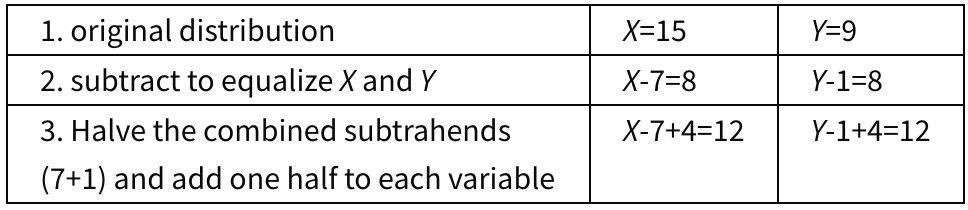
Question c) involves determining the ratio between X and Y.

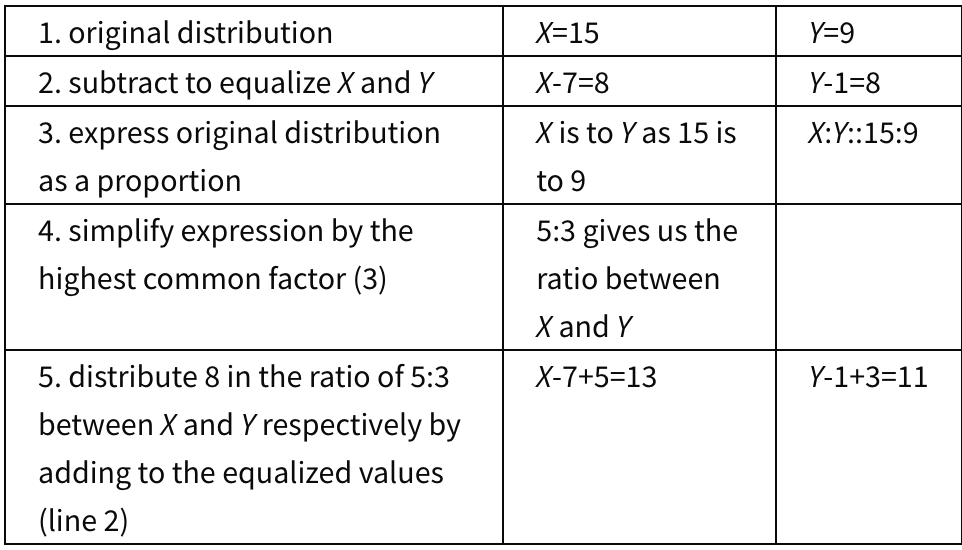
Now for the verbal narrative, albeit abbreviated. Approaching the ruined village of Sippar on their travels, the narrator and his companion, Beremiz, also known as “the Man Who Counted,” happened upon a wretch who had been robbed and wounded by bandits. For all his wealth stored in Baghdad, this injured man, Salem Nasair, could go no further without sustenance. The narrator had three loaves with him, and Beremiz had five. They promised to share their food with the man, who in turn promised to pay them, on arrival in Baghdad, eight gold coins for their eight loaves. On this understanding, they proceeded to the city. Restored to his wealth, the sheikh went to repay his saviors by handing the narrator three coins for his three loaves, and Beremiz five for his. But the Man Who Counted strongly objected, claiming that he deserved seven coins and his partner only one. Here was his reasoning: he, Beremiz, had given the hungry man two and one third of his loaves (7/3), consuming two and two thirds himself (8/3), while the narrator, also having consumed two and two thirds (8/3), had given the hungry man only one third of one loaf (1/3). Persuaded by this logic, Salem Nasair gave the narrator one coin and seven to the Man Who Counted. But then—

“This division,” replied the Man Who Counted, “—seven for me and one for my friend—is, as I just proved, mathematically valid (certa), but it is not perfect (perfeita) in the eyes of the Almighty.” And, gathering the coins again, he divided them into two equal shares, handing me four and keeping four.
(Tahan, O Homem 31; translation adapted from Tahan, The Man 17)

There are meanings here about generosity that exceed the bare computations. The story seems to imply that we should overlook nitpickingly precise divisions by sharing freely what we have. We may even infer from it that love for a fellow human observes a higher, non-quantifiable law and cannot be measured.

Yet the computations in turn challenge that reading. In the fictional story, the first distribution is 5:3, the second 7:1, and the third 4:4. These map onto the distributions in the math problem above as c, a, and b, respectively. Ironically enough, the first proposed distribution in the story, that attempted by the sheik, corresponds to the third and most complicated calculation, which divides the gold in accordance with the ratio between Beremiz’s and the narrator’s original portions of bread. The first and easiest calculation is that initially proposed by Beremiz. By his brute logic, the gold should be so divided as to restore the status quo, where one man owns more than another, and where inequitable distribution of resources is an unexamined given that lies outside the frame of the transaction.

The reasoning for the second distribution, where both men share equally, is almost as straightforward as the first solution. But the numbers can be told differently to arrive at the same distribution:

Retelling the story by the logic of this method of distribution, we no longer take from the one who has more and give to the one who has less; instead, each gives the other half his wealth. In God’s higher math, X and Y reciprocate to take each other’s share, thereby equalizing each man’s portion. Far from implying, as the fictional story does, that mathematics can take you only thus far, then to be superseded by the higher force of love, Beremiz’s “generosity” is as mathematically justifiable as the “valid” distribution he had earlier advocated. Mathematics does not get superseded. The sly moral of this tale is that there is nothing, not even friendship, that cannot be measured.

Conclusion

The history of Western mathematics tells of a “hesitating progress” from a rudimentary algebra whose terminology existed, as Jens Høyrup phrases it, “close to earth” (8), to the symbolically denotated abstract objects of modern mathematics, where the actors of its conceptual plots have bodies only by analogy. Even as symbolic notation detaches from determinate number to ascend into abstraction, the tight breathing of the math anxious acts as inescapable reminder of their somatic limitations. Outsiders in the math community by dint of their bodies, they experience the effects of exclusion on those same bodies: constricted chest, perspiration, the flush of embarrassment. We have attempted to re-embody the characters of math stories, not to reduce abstraction, but to accentuate its deft strength. By accommodating Beremiz’s “perfect” division, the body of reasoning simply flexes and stretches. As rhetorically mobile as ordinary language, the precision of mathematics is matched only by its suppleness. No problem is ever fully exhausted (Polya 15), for there is always another route to vary the solution, always one other way to tell the story.

It is impossible to take breathing out of any narrative flow, be it Louis Armstrong storying on the trumpet or the release of tension felt as a math problem unravels itself. Retelling stories from multiple sides slows the tempo and creates the space needed for deep understanding. Rarely, however, will a traditional curriculum afford such opportunity to reiterate. Always under pressure to take in the next topic, the disenfranchised can’t catch a breath: long exhalations become short and shallow as anxiety sets in. Those deep breathing exercises recommended as therapeutic interventions need to be taken as figuratively as they are literally. Put the stories back in math.